I was showing a friend the sun today, and he asked how big the sunspots were. I told him I’d send him a photo of the Venus transit across the face of the Sun last year, so he could get a feel for the sunspots relative to the size of the Earth. I told him he’d have to take into account, the fact that Venus is a considerable distance from the Sun, and, thus, it appears larger than it would if it were at the surface of the Sun like the sunspots. I thought I’d do some calculations to give some absolute numbers on the diameter of the spots based on how big Venus appears in the photos. Here they are for all to see.
Some quick facts:
- The Earth’s mean distance from the Sun is about 150,000,000 km.
- Venus’ mean distance from the Sun is 108,000,000 km.
- The Sun’s approximate radius is 700,000 km.
- The Earth’s mean radius is 6371 km.
- Venus’ mean radius is 6052 km.
OK. I’m going to ignore:
- Uncertainties
- The orbits of the Earth and Venus are not perfectly circular, and they precess around the Sun. (In other words, the orbits are ovals and the long axis of the oval itself rotates around the sun.) This means the distance between the Earth and Venus varies by almost 7,000,000 km.
I’m going to calculate the size of the sunspot two different ways to check the work. Let’s go with the simplest method first.
First method: Relative size of the sunspot and the Sun in the image.
Using the relative size of the sunspot and the sun in the photo, we can just calculate the ratio in pixels and apply it to the known size of the Sun in km to determine the sunspot size in km.
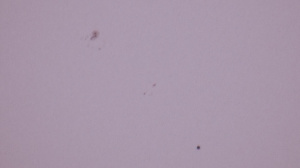
The image I’m publishing is scaled down and compressed using a lossy compression which is going to fuzz things a bit, so any measurement you would do will vary from the uncompressed master image I used for measurements. In the master image, the round sunspot to the below left of center appears to be between 25-26 pixels in diameter when measuring the penumbra (the gray outer region of the spot) , and the Sun itself appears to be between 1180 and 1186 pixels in diameter.
The ratio of the average size in pixels is then: ((25+26)/2) / ((1180+1186)/2) = 0.02156
Applied to a diameter of 1,400,000 km for the Sun produces a size of: 0.02156 * 1,400,000km = 30184 km.
Second method: Use trigonometry and the known sizes and distances of objects.
Given the above facts, approximate distance of an observer on Earth from the surface of the Sun is:
150,000,000 – 700,000 – 6371 km = 149,293,629 km
The radius of the Earth is really insignificant here because the variability of the distance between the Earth and the Sun (approx. 5,000,000 km) is far larger (which itself is not too significant because the variability is much less than the average distance), but I threw it in to show it has been considered.
In the master image, Venus at a distance of 150,000,000 – 108,000,000 – 6371 km (41,993,629) from the observer appears to be between 36 and 37 pixels in diameter.
- From the Earth, Venus appears as 2 * atan(6052 / 41,993,629) = 0.01651 degrees.
- At the Sun, Venus would appear 2 * atan(6052 / 149,293,629) = 0.004645 degrees
- The ratio between those two angles is 0.004645 / 0.01651 = 0.2813.
- If we apply this ratio to the pixel size of Venus, we can determine how many pixels it would be if it were at the distance of the Sun’s surface. This results in an average size of 10.25 pixels.
- Previously, we measured the sunspot to be 25-26 pixels, so the sunspot must be (25.5 / 10.25) * (6052 * 2) km = 30,112 km.
So, both methods produce a value of about 30,000 km (about 2.5x the size of Venus or the Earth). The difference could be attributed to:
- The real distance between Earth and Venus on the day the photo was taken may have been quite different from the rough estimate that was used. A rough estimate for the Earth-Sun distance was also used, but the same value was used in both calculations, so that shouldn’t cause an issue.
- The pixel measurements are a little fuzzy. When you examine the image closely you see that the edges of both the Sun and Venus are a little fuzzy. Some of this is certainly a result of the BayerFilter on the CMOS sensor in my digital SLR, and some of it might also be the atmospheric distortion above the surfaces of the object.
- The way the calculations were done assume that the Sun as measured is the same distance from the observer as the sunspot, but in fact the diameter of the sun being measured is an additional 700,000 km farther making it appear smaller.

Venus transiting the sun on 2012-06-05 22:28 UTC. The image also has sunspots which allows us to determine how big the sunspots are compared to the known size of Venus.